Explorationsaufgaben sind Erkundungsaufgaben. Bei diesen Aufgaben handelt es sich in der Regel um Problemlöseaufgaben, die unterschiedlich (kognitiv) anspruchsvoll sein können.

Ein Beitrag von Manuel Garcia Mateos, Landesinstitut für Pädagogik und Medien Saarland
– MaLeNe-Koordinator Saarland –

Die Schülerinnen und Schüler sollen hier neben fachlichen Inhalten auch noch andere Sachen lernen, die für den Mathematikunterricht und die Mathematik sehr wichtig sind, z. B.

Fragen stellen:
„Wieso ist das so?“, „Ist das immer so?“
Herangehensweisen erlernen:
„Ich setze mal Zahlen ein“, „Ich fertige eine Tabelle oder Skizze an“, „Ich betrachte Spezialfälle oder einfache Fälle. Erst dann verallgemeinere ich.“
Aufgabenstellung verstehen:
„Was soll ich hier tun? Ich mach mal eine Skizze“, „Hab ich den Text verstanden? Welche Begriffe kenne ich, welche nicht?“, „Wo kann ich nachschlagen? Wen kann ich fragen?“
Ideen und Wege sowie Irrwege dokumentieren und reflektieren:
„Ich rechne mal nach“, „Was passiert in den Extremfällen?“, „Hab ich schon mal so eine Problemstellung gehabt und gelöst? Wie habe ich das gemacht?“, „Dieser Weg klappt nicht. Wieso nicht?“
Strategien entwickeln, die in Zukunft helfen könnten:
„Aha, mit Tabellen kann ich mir ganz schnell einen numerischen Überblick verschaffen“, „Eine Skizze hilft mir“, „Ich fange mal mit einfachen Zahlen und einfachen Fällen an und ersetze später die Zahlen durch Variablen.“
Neugier entwickeln:
„Das ist ja seltsam. Geht das auch mit anderen Figuren?“, „Dieser Zusammenhang gilt bei Nullstellen. Wie sieht es denn mit den Extremstellen aus?“, „Das gilt bei 90°. Wie sieht es denn bei 45° aus?“
Schönheit und Sinnhaftigkeit der Mathematik erfahren:
„Das ist ja ein schönes/ein seltsames Ergebnis.“, „Die Mathematik hilft mir einen Überblick zu verschaffen und Sachen abzuschätzen.“
Mit Technologien und anderen Hilfsmitteln umgehen:
„Ich löse das Beispiel mal für verschiedene Zahlen mit dem CAS“, „Ich lass mir mal den Graphen zu der Funktion für verschiedene Werte anzeigen“, „Ich muss hier eine Gleichung lösen, die mich einfach nur Zeit kostet.“
Über den Lösungsweg sprechen und diesen darstellen:
„Ok. Wie erkläre ich das so, dass andere meine Lösung verstehen? Ich hab ja Zeit und Energie investiert und bin stolz auf meine Lösung.“, „Habe ich verstanden, wie ich das gemacht habe? Könnte ich das erklären?“, „Wenn ich mir später die Aufgabe noch mal anschaue, dann sollte ich das so aufgeschrieben haben, dass ich das auch lesen kann. Ich formuliere also meine Ideen und Herangehensweisen in Worten.“
Arbeiten mit anderen und andere Blickwinkel aufnehmen:
„Lasst uns viele Beispiele untersuchen. Wer macht was?“, „Wie könnten wir an die Lösung gehen?“, „Ich komm hier nicht weiter. Hast du eine Idee?“, „Von einer geteilten Idee hat jeder was.“
…

Es ist klar, dass der Erwerb von fachlichen Inhalten eine zentrale Aufgabe des Mathematikunterrichts ist. Explorationen machen nur im Zusammenhang mit fachlichen Inhalten Sinn und dürfen nicht losgelöst davon im Mittelpunkt stehen. Zentrales Ziel der Explorationsaufgaben ist das Erkunden von mathematischen Zusammenhängen und Beziehungen. Es geht nicht zentral um ein Einüben von Rechenfertigkeiten. Daher sind Explorationsaufgaben sehr oft (relativ) allgemein, offen und textlich nicht einfach formuliert. Explorationsaufgaben können also im Unterricht sehr gut dazu verwendet werden, um über Mathematik zu sprechen und aufzuzeigen, wie Mathematik funktioniert. Sie sind explizit Bestandteil der Bildungsstandards für die Allgemeine Hochschulreife (siehe KMK 2012, S. 11) der KMK, denn mithilfe von Explorationsaufgaben kann gemäß der drei WINTERschen Grunderfahrungen* aufgezeigt werden, dass Mathematik nützlich ist, schön ist und ideenreich ist. Auch die Rolle der digitalen Medien wird in den Bildungsstandards bei diesen Aufgaben explizit hervorgehoben (siehe KMK 2012, S. 13).

Beispielaufgabe

Im Folgenden soll an einem Beispiel der Unterrichtseinsatz von Explorationsaufgaben mithilfe des CAS veranschaulicht werden:

Betrachte ein Polynom \(P\) mit
\(P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdot \cdot \cdot+a_{1}x+a_{0}\)
und das dazu “gespiegelte” Polynom \(Q\) mit
\(Q(x)=a_{0}x^{n}+a_{1}x^{n-1}+\cdot \cdot \cdot+a_{n-1}x+a_{n}\),
jeweils mit \(a_{n}\neq 0, a_{0}\neq 0\).

Gibt es einen Zusammenhang zwischen den Nullstellen des Polynoms \(P\) und denen des Polynoms \(Q\)?

Umsetzung der Beispielaufgabe im Unterricht

Bei diesem Beispiel geht es um den Zusammenhang zwischen den Nullstellen zweier Polynome. Die Problemstellung ist für Schülerinnen und Schüler nicht einfach, da zum einen Begriffe und Formalismen vorkommen, die sie nicht gewohnt sind, und zum anderen keine konkreten Zahlen vorgegeben sind. Der erste Schritt ist demnach, zu verstehen, was hier eigentlich gefragt ist. Eine wesentliche Hilfe ist der didaktische Dreiklang:

1) Vom Konkreten zum Abstrakten,
2) vom Speziellen zum Allgemeinen und
3) vom Einfachen zum Komplexen.

Der wesentliche Schritt ist, eine Vermutung über die Beziehung einzelner Nullstellen mithilfe des CAS zu erkunden, zu formulieren und zu verifizieren. Arbeitsteilig können die Schülerinnen und Schüler mithilfe des CAS viele konkrete Beispiele betrachten und entsprechende Vermutungen
formulieren. Im ersten Schritt können z. B. die Nullstellen linearer Funktionen mit \(f(x)=ax+b\) und \(g(x)=bx+a\) untersucht und Zusammenhänge formuliert werden, in einem zweiten Schritt dann entsprechend quadratische Funktionen.

Anscheinend sind die Nullstellen der „gespiegelten“ Funktionen gerade die Kehrwerte der ursprünglichen Funktionen. Das CAS bestätigt diese Vermutung, wobei die Interpretation der Lösung bei allgemeinen quadratischen Funktionen schon schwierig ist. Schülerinnen und Schüler erkennen in der Regel aus der allgemeinen Darstellung nicht, dass die Lösungen reziprok zueinander sind. Daher ist es nicht ratsam, die “Mächtigkeit” des CAS bei Explorationen direkt vollständig auszunutzen. Ist das nun immer so? Wie sieht es bei kubischen Funktionen aus, für die die Schülerinnen und Schüler keine allgemeine Lösungsformel haben? Auch hier hilft das CAS weiter.

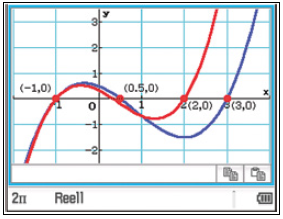
Im nächsten Unterrichtsschritt muss versucht werden, die Vermutung zu formulieren und diese rechnerisch zu begründen bzw. zu beweisen. Der Beweis geschieht durch Nachrechnen.

Situation:
Betrachten wir ein Polynom \(P\) mit
\(P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdot \cdot \cdot+a_{1}x+a_{0}\)
und das dazu “gespiegelte” Polynom \(Q\) mit
\(Q(x)=a_{0}x^{n}+a_{1}x^{n-1}+\cdot \cdot \cdot+a_{n-1}x+a_{n}\),
jeweils mit \(a_{n}\neq 0, a_{0}\neq 0\).

Vermutung:
Es gibt einen Zusammenhang zwischen den Nullstellen von \(P\) und den Nullstellen von \(Q\). Ist \(r \neq 0\) eine Nullstelle von \(P\), dann ist \(1/r\) eine Nullstelle von \(Q\).

Beweis:
Ist \(r\) eine Nullstelle von \(P\), \(P(r)=0\), dann ist
\(Q(\frac{1}{r})=a_{0}(\frac{1}{r})^{n}+a_{1}(\frac{1}{r})^{n-1}+\cdot \cdot \cdot+a_{n-1}(\frac{1}{r})+a_{n}\).

Wird die Gleichung mit \(r^{n} \neq 0\) multipliziert, so ist
\(r^{n} Q(\frac{1}{r})=a_{0}+a_{1}r+\cdot \cdot \cdot+a_{n-1}r^{n-1}+a_{n}r^{n}=P(r)=0\).

Ausblick

Die Nullstellen der gespiegelten Funktion entstehen geometrisch durch eine Inversion am Einheitskreis, Es fragt sich nun, wie es mit anderen besonderen Stellen bei Polynomen, etwa Extrem- und Wendestellen ist. Gibt es da auch einen entsprechenden Zusammenhang?

Explorationsaufgaben bieten die Möglichkeit, aktiv zu lernen, und die Chance, Mathematik zu machen abseits von Kalkülen. Das CAS ist hierbei ein hilfreiches Werkzeug, das den Explorationsprozess unterstützt.

*Nach Heinrich Winter (1928-2017) aus: Mitteilungen der Gesellschaft der Mathematik – Nr. 61, S. 37-46 (1995)

Dieser Beitrag stammt ursprünglich aus dem Casio Forum 2019/1.