Eine Interpolation scheint naheliegend, um Daten mittels einer Funktion zu beschreiben. Die so ermittelte Funktion erlaubt es wiederum, unterschiedliche Fragen (beispielsweise nach Extremwerten oder Änderungsraten) mithilfe der üblichen Verfahren der Kurvendiskussion zu beantworten. Nicht alle Datensätze sind geeignet, ein sinnvolles, kontinuierliches Modell zu erstellen – dies soll einmal im Kontext von Temperaturmessungen und einmal im Kontext des monatlichen Umsatzes eines Unternehmens untersucht werden.
Ein Beitrag von Jörg Kreyser, Gymnasium Oldenfelde (Hamburg)
– MaLeNe-Koordinator Hamburg –

Temperaturmessungen
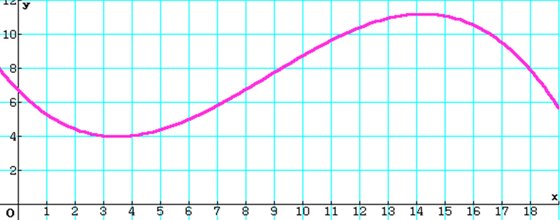
Gegeben sind die Temperaturdaten vom 2. November 2021 aus Hamburg-Fuhlsbüttel:

Die Interpolation dieser Messpunkte liefert die Funktion \(t\) mit
$$t(x)=-\frac{5}{432} x^3 + \frac{221}{720} x^2 -\frac{41}{24} x + \frac{67}{10}$$
An diese Funktionen lassen sich Fragen unterschiedlicher Art stellen (und beantworten):
- Wie groß ist die maximale Temperatur in diesem Modell?
- Wann ist die Temperaturänderung in diesem Modell am größten?
- Wie groß ist die Durchschnittstemperatur in diesem Modell im Zeitintervall [\(a; b\)]?
Umsatzmessungen
Die Messwerte werden jetzt in einem neuen Zusammenhang gelesen.
Der Umsatz eines Unternehmens in den ersten vier Monaten eines Jahres ist in der folgenden Tabelle dargestellt:

Auch diese Daten lassen sich interpolieren:
$$V(x)=-\frac{5}{2} x^3 + \frac{371}{20} x^2 -\frac{797}{20} x + \frac{61}{2}$$
Die zugrundeliegenden Messungen erfolgen nicht an Zeitpunkten, sondern über Zeitintervalle. Im ersten Beispiel liefert die Modellfunktion Temperaturen \(t(x)\) zu verschiedenen Zeitpunkten \(x\). In dem Sachzusammenhang Umsatz wird der Wert 6,7 zwar dem Zeitpunkt 1 zugeordnet, ist aber das Ergebnis einer Messung über ein Zeitintervall, nämlich dem ersten Monat. Anders gesagt, werden dem Zeitpunkt 1 alle (gedachten) Umsätze im Intervall von 0 bis 1 zugeordnet.
Daraus lässt sich die Bedeutung des Wertes \(V(\)1,5\()\) als Umsatz in der Zeit von der Mitte des ersten Monats bis zur Mitte des zweiten ableiten, also im Intervall von 0,5 bis 1,5. Der Funktionswert \(V(x)\) entspricht dem Umsatz der vorangegangenen 30 Tage, also im Intervall [\(x−1; x\)].
Die Größe \(V'( x_{0})\) ist die Änderung des durchschnittlichen Umsatzes und nicht die Umsatzrate.
Die Größe \( \frac{1}{x_2−x_1} \int_{x_1}^{x_2} V(x) \, dx \) ist ein Durchschnittswert, aber nicht der durchschnittliche Umsatz.

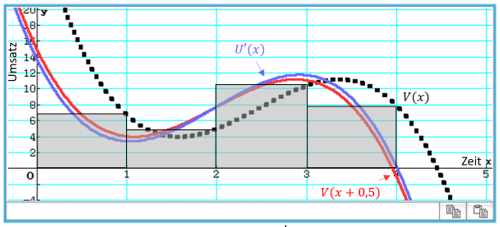
Die oberen Kanten des Säulendiagramm lassen sich als Darstellung des durchschnittlichen monatlichen Umsatzes interpretieren.
Mit der Modellfunktion sollen in der Regel Fragen beantwortet werden wie:
- Wann ist in diesem Modell der Umsatz maximal, genauer: die maximale Intensität des Umsatzes?
- Wann ist die Umsatzänderung in diesem Modell am größten?
- Wie groß ist der durchschnittliche Umsatz in diesem Modell im Zeitintervall [\(a ; b\)]?
All diese Fragen können nicht mit der Funktion \(V\) beantwortet werden. Bei \(V(x)\) ist \(x\) ein Zeitpunkt, der Funktionswert aber eine Aussage über ein Zeitintervall [\(x – 1 ; x\)]. Eine angemessene Darstellung der Messwerte entspricht eher einem Säulendiagramm, das die Messwerte als konstante Funktionswerte im Intervall ausweist.
Die Lösung des Problems besteht darin, dass man die kumulierten Umsatzwerte betrachtet.

Die Interpolation liefert eine stetige Umsatzfunktion \(U\) mit
$$U(x)= -\frac{5}{8} x^4 +\frac{74}{15} x^3 – \frac{451}{40} x^2 -\frac{41}{3} x$$
\(U(x)\) ist der Umsatz vom Zeitpunkt 0 bis zum Zeitpunkt \(x\). Diese Funktion ist eine Bestandsfunktion, während \(V\) die Differenz von Bestandswerten angibt. Für alle \(n \in \big\{1, 2, 3, 4\big\}\) gilt: \(V(n)=U(n)−U(n−1)\)
Die Funktion \(U’\) ist dann eine Funktion, mit der die obigen Fragestellungen beantwortet werden können.
Der Wert der Ableitung \(U'(x)\) entspricht der Änderungsrate des Umsatzes (dem momentanen Umsatz pro Zeiteinheit), und mit
$$\frac{1}{x_2−x_1} \int_{x_1}^{x_2} U'(x) \, dx = \frac{U( x_2)−U(x_1)}{x_2−x_1}$$
wird der durchschnittliche Umsatz im Intervall [\(x_1;x_2\)] berechnet.
Zusammenfassung
Sind die Messwerte das Ergebnis von Messungen in Zeitintervallen, die sich aneinanderreihen (hier: Messungen über jeweils einen Monat), so scheint es nur bedingt sinnvoll, diese Messwerte in ein stetiges Modell zu überführen.
Die Messwerte können aber sinnvoll genutzt werden, indem sie aufsummiert werden. Die aufsummierten Werte entsprechen hier dem Umsatz vom Zeitpunkt \(t = 0\) bis zum angegebenen Zeitpunkt. Daraus lässt sich ein kontinuierliches Modell erstellen, das sich sinnvoll(er) interpretieren lässt. Die ursprünglichen Messwerte sind dann die Werte der Differenzfunktion \(\Delta\) mit \(\Delta (x)=U(x)−U(x−1)\) für ganzzahlige \(x\) von 1 bis 6.