Die Nutzung regenerativer Energien hat in den letzten Jahren zunehmend an Bedeutung gewonnen und wird mit Sicherheit weiter vorangetrieben werden müssen. Hierbei haben Windenergieanlage (WEA) besonders in Norddeutschland aufgrund günstiger geographischer und meteorologischer Bedingungen eine besondere Bedeutung.

Ein Artikel von Ralf Hoheisel, Berufsbildende Schule ME Hannover
– MaLeNe-Koordinator Niedersachsen –

In diesem Artikel sollen die mathematisch-physikalischen Grundlagen der windenergetischen Zusammenhänge erarbeitet und visualisiert werden, insbesondere
• die Windleistung, die in der bewegten Luftmasse enthalten ist.
• die Leistung, die von einer WEA abgegeben wird.
• die maximale Leistung einer WEA.
• der theoretische Wirkungsgrad einer Windkraftanlage.

Bild 1: Darstellung der Strömungsverhältnisse einer WEA

Bild 2: Visualisierung mit dem ClassPad II

Wind enthält kinetische Energie, $W_{kin}=\frac{1}{2}m\cdot v^2$, bzw.

$dW_{kin}=\frac{1}{2}dm\cdot v^2$, mit der Masse $dm=\rho \cdot dV$ und dem Volumen $dV=A \cdot ds$.

Damit ist $dW_{kin}=\frac{1}{2}\rho \cdot dV \cdot v^2 = \frac{1}{2}\rho \cdot A \cdot ds \cdot v^2 $.

Leistung ist Energie (Arbeit) pro Zeit, also $P=\frac{dW_{kin}}{dt} = \frac{1}{2}\rho \cdot A \cdot \frac{ds}{dt} \cdot v^2 = \frac{1}{2}\rho \cdot A \cdot v \cdot v^2$.

$$P_0=\frac{1}{2}\rho \cdot A \cdot v^3$$
Windleistung $P_0$ mit Wirkfläche $A$, Luftdichte $\rho$ und Windgeschwindigkeit $v$

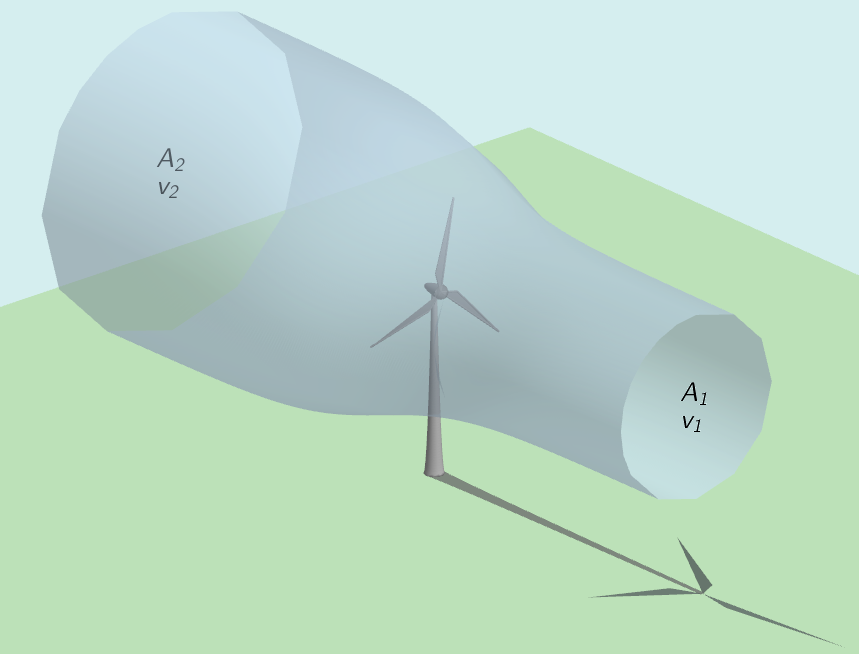
Möchte man dem Wind durch eine WEA Leistung entziehen, so muss man seine Strömungsgeschwindigkeit $v$ verlangsamen.

$P_{ab}=P_2-P_1$

$P_1$: Windleistung vor der WEA, Windgeschwindigkeit $v_1$
$P_2$: Windleistung nach der WEA, Windgeschwindigkeit auf $v_2$ abgebremst

Das gelingt nur, wenn die Massenströme $\dot{m}_{v_1}$ vor und $\dot{m}_{v_2}$ nach der Leistungsentnahme gleich sind (Kontinuitätsbedingung).

$\dot{m}=\frac{dm}{dt}$ mit $dm=\rho \cdot dV = \rho \cdot A \cdot ds$

$\dot{m}=\rho \cdot A \cdot \frac{ds}{dt}=\rho \cdot A \cdot v$

$\dot{m}=\dot{m}_{v_1}=\dot{m}_{v_2} \Rightarrow \rho \cdot A_1 \cdot v_1 = \rho \cdot A_2 \cdot v_2 \Rightarrow A_1 \cdot v_1=A_2 \cdot v_2$,

da die Dichte unverändert angenommen wird.

Ändert sich die Windgeschwindigkeit nach der WEA durch Leistungsentnahme, dann muss sich auch die Wirkfläche ändern, es kommt also zu einer Aufweitung der Wirkfläche.

Für die abgegebene Leistung gilt dann:

$P_{ab}=\frac{1}{2}\rho \cdot A_1 \cdot v_1^3-\frac{1}{2}\rho \cdot A_2 \cdot v_2^3$

$P_{ab}=\frac{1}{2}\rho \cdot A_1 \cdot v_1 \cdot v_1^2-\frac{1}{2}\rho \cdot A_2 \cdot v_2 \cdot v_2^2$

$P_{ab}=\frac{1}{2}\dot{m} \cdot v_1^2-\frac{1}{2}\dot{m} \cdot v_2^2$

$P_{ab}=\frac{1}{2}\dot{m} \cdot (v_1^2-v_2^2)$

Die Windgeschwindigkeit an der WEA (am Ort der Leistungsentnahme) ist der Mittelwert aus $v_1$ und $v_2$ (Theorem von Froude und Rankine), hier ohne Beweis.

$\overline{v}=\frac{1}{2}(v_1+v_2)$

Damit gilt für den Massenstrom $\dot{m}=\rho \cdot A \cdot \overline{v}$:

$\dot{m}=\frac{1}{2}\rho \cdot A \cdot (v_1+v_2)$

Für die Leistung folgt dann

$P_{ab}=\frac{1}{2}\cdot \frac{1}{2}\rho \cdot A \cdot (v_1+v_2) \cdot (v_1^2-v_2^2)$

$$P_{ab}=\frac{1}{4}\rho \cdot A \cdot (v_1+v_2) \cdot (v_1^2-v_2^2)$$
Leistungsabgabe in Abhängigkeit der Windgeschwindigkeit $v_2$ nach der WEA

Die Zusammenhänge wurden bereits von Albert Betz* 1926 erstmalig veröffentlicht.

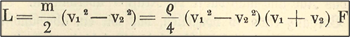
Bild 3: Im Original von Albert Betz notierte Gleichung

$$P_{ab}(v_2)=\frac{1}{4}\rho \cdot A \cdot (v_1+v_2) \cdot (v_1^2-v_2^2)$$
Windleistung in Abhängigkeit der Windgeschwindigkeit $v_2$ nach der WEA

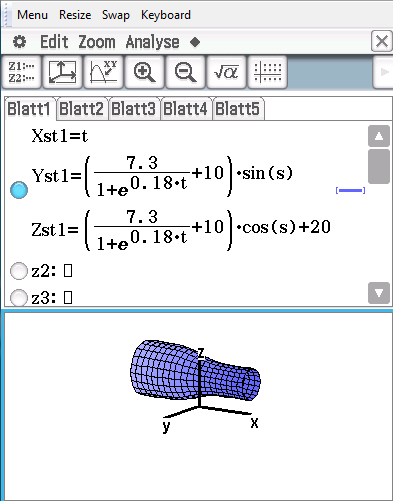
Die mathematische Beschreibung der Windleistung in Abhängigkeit der Windgeschwindigkeit $v_2$ nach der WEA ist ein gutes Beispiel für eine ganzrationale Funktion 3. Grades, die in der Technik Verwendung findet. Interessant ist in diesem Zusammenhang die von Betz gewählte Notation in Linearfaktorenschreibweise, die auch noch die 3. binomische Formel beinhaltet.

Vereinfacht man die oben dargestellte Form durch Einsetzen von realistischen Werten für $\rho$, $A$ und $v_1$ und verzichtet ggf. auf die Herleitung, so eignet sich diese Funktionsgleichung gut zum Einstieg in die Thematik ganzrationaler Funktionen 3. Grades.

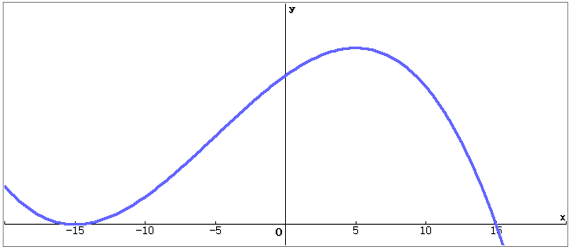
Offensichtlich gibt es eine Windgeschwindigkeit $v_2$ , bei der die Leistungsabgabe maximal wird, dort gilt $P_{ab}^{\prime}(v_2)=0$.

Falls diese Funktion als Einstieg in ganzrationale Funktion 3. Grades gewählt wurde, steht die Differentialrechnung noch nicht zur Verfügung. Dennoch kann das Problem mithilfe der Technologie durch graphische Bestimmung des Hochpunktes gelöst werden.

$P_{ab}^{\prime}(v_2)=0 \Rightarrow \frac{1}{4}\rho \cdot A \cdot \left[
(v_1^2-v_2^2) + (v_1+v_2) \cdot (-2v_2) \right] =0 $

$(v_1^2-v_2^2) + (v_1+v_2) \cdot (-2v_2) =0$

$v_1^2-v_2^2 – 2v_1v_2 – 2v_2^2=0$

$-3v_2^2-2v_1v_2+v_1^2=0 \Rightarrow v_2^2+\frac{2}{3}v_1v_2-\frac{1}{3}v_1^2=0$

$v_{2_{1/2}} = -\frac{1}{3}v_1 \pm \sqrt{\frac{1}{9}v_1^2+\frac{1}{3}v_1^2} =
-\frac{1}{3}v_1 \pm \sqrt{\frac{4}{9}v_1^2} =
-\frac{1}{3}v_1 \pm \frac{2}{3}v_1$

$ \Rightarrow v_{2_1}= \frac{1}{3}v_1$ und $v_{2_2}=-v_1$, wobei $v_{2_2}=-v_1$ sinnlos ist.

Die WEA gibt ihre maximale Leistung ab, wenn die Windgeschwindigkeit nach der Anlage auf $\frac{1}{3}$ der Windgeschwindigkeit vor der Anlage abgebremst wird.

Setzt man die von der WEA abgegebene Leistung $P_{ab}$ ins Verhältnis zur Windleistung $P_0$, dann erhält man den Leistungsbeiwert $c_P$, der sein Maximum bei $v_2=\frac{1}{3}v_1$ hat.

$$c_P=\frac{P_{ab}(v)}{P_0}$$

$$c_P=\frac{\frac{1}{4}\rho \cdot A \cdot (v_1+v_2) \cdot (v_1^2-v_2^2)}{\frac{1}{2}\rho \cdot A \cdot v_1^3}$$

$$c_{P_{max}}=\frac{\frac{1}{4}\rho \cdot A \cdot (v_1+\frac{1}{3}v_1) \cdot (v_1^2-\frac{1}{9}v_1^2)}{\frac{1}{2}\rho \cdot A \cdot v_1^3}
=\frac{\frac{1}{2}(\frac{4}{3}v_1) \cdot (\frac{8}{9}v_1^2)}{v_1^3}=
\frac{16}{27} \approx 59,3 \%$$

Der maximale Wirkungsgrad einer WEA, unabhängig von der technischen Ausführung, kann also nicht mehr als knapp 60% betragen.

*Albert Betz, Wind-Energie und ihre Ausnützung durch Windmühlen, 1926

Dieser Beitrag stammt ursprünglich aus dem Casio Forum 2020/1.