Seit 2011 gibt es in Bayern neben dem traditionellen Abitur auch die Möglichkeit, die schriftliche Prüfung unter Verwendung eines Computeralgebrasystems (CAS) zu schreiben. Über die Chancen, die sich dadurch für den Unterricht eröffnen, gibt es bereits zahlreiche Vorschläge und verschiedene Untersuchungen (etwa Barzel et al. 2005). Auch auf die damit einhergehenden veränderten Anforderungen an CAS-Prüfungsaufgaben wurde schon eingegangen (vgl. Pallack 2007).

Diese beiden Aspekte des CAS-Einsatzes haben mehr oder weniger das Unterrichten von Mathematik im Blick. Wie Lösungen in Klausuren und Prüfungen aufgeschrieben werden sollen, ist für Schülerinnen und Schüler sowie für Lehrerinnen und Lehrer eine wichtige Frage (vgl. Beck 2015). Die Herausforderungen der veränderten Dokumentationskultur gegenüber traditionellen Prüfungen mit Papier und Bleistift sollen im Folgenden ausgehend von einer Beispielaufgabe aus dem bayerischen CAS-Abitur 2014 auch anhand von authentischen Schülerlösungen dargestellt werden.

Ein Artikel von Johannes Beck, Julius-Maximilians Universität Würzburg

Lösungsdokumentationen unter wissenschaftlicher Betrachtung

Eine Beispielaufgabe aus dem CAS-Abitur Bayern 2014:

Gegeben ist die Polynomfunktion dritten Grades s, die in einem bestimmten Bereich modellhaft eine Autobahnausfahrt beschreiben soll. Bestimmen Sie den Punkt, in dem die Rechtskurve in eine Linkskurve übergeht.

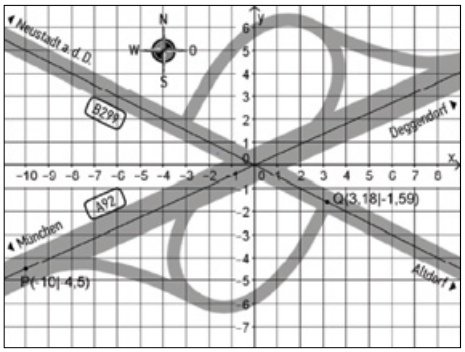
Für Schülerinnen und Schüler stellt sich neben der inhaltlichen Bearbeitung die Frage, was sie ihren Lehrkräften mitteilen müssen, damit diese die Lösung verstehen und sie adäquat bewerten können.

Diese Frage soll zwei Aspekte illustrieren: Zum einen stellen Lösungsdokumentationen Texte dar (vgl. Beck/Maier 1996), die der Kommunikation zwischen dem Schreiber (Textproduzent) und einem Leser (Textrezipient) dienen. Der Textproduzent (hier Schülerinnen und Schüler; oft aber auch Lehrerinnen und Lehrer) orientiert sich an seinem Wissen über Kommunikation, um seine „Botschaft“/Nachricht zu übermitteln.

Zum anderen orientiert er sich auch an Normen, zieht also sein Wissen darüber heran, wie „Lösungsdokumentationen auszusehen haben”. Der zweite Aspekt besteht also darin, dass Lösungsdokumentationen beispielsweise folgenden Normen unterliegen.

Rechtliche Vorgaben könnte es in Form von Mitteilungen der Kultusministerien geben, in denen Richtlinien festgelegt werden. Von offizieller Seite angebotene Beispieldokumentationen zählen hierzu genauso wie die verbindliche Richtlinie, dass keine elektronischen Dokumentationen im Abitur abgegeben oder bewertet werden dürfen.
Schülerinnen und Schüler stellen mathematische Inhalte spätestens mit Beginn der Grundschule auch auf einem gewissen formalen Level schriftlich / symbolisch dar. Die dabei erlernten Regeln werden natürlich auch im CAS-Unterricht teilweise fortgeführt.
Lehrer haben Vorstellungen zu CAS-Dokumentationen und geben diese weiter (Beispiel: Sollen/dürfen CAS-Befehle notiert werden? -> s.u.).

Lehrkräfte stellen aber auch oft die Frage: Wie sollen wir dokumentieren lassen? Diese Frage ist deshalb berechtigt, da die Art und Weise, wie dokumentiert werden soll, sich nicht innermathematisch-logisch begründen lässt, sondern, wie gerade aufgezeigt, mehr als „nur” Mathematik umfasst.

Schülerbeispiele

Obige Überlegungen sind im Rahmen einer Untersuchung von Schülerlösungen aus dem Abitur mit CAS seit 2014 hervorgegangen. Hierbei bestand der erste Schritt darin, herauszufinden, wie Schülerinnen und Schüler dokumentieren, welche vielfältigen Formen es evtl. gibt und welche Probleme oder Schwierigkeiten ggf. entdeckt werden können. Folgende drei Abbildungen zeigen, was Schülerinnen und Schüler im Abitur aufgeschrieben haben:

Alle Lösungen verwenden dieselbe mathematische Idee: das Bestimmen des Wendepunktes mittels zweiter Ableitung. Allerdings erklärt die erste Lösung (Abb. 1) diese Idee vor der Ausführung explizit in einem Satzfragment. Die zweite Lösung dagegen erklärt die Bedeutung der Ergebnisse (wenn auch die Lösung nicht ganz vollständig ist) verbal in Form eines Antwortsatzes, der den Rückbezug zum Sachkontext herstellt. Dies ist in der dritten Lösung nicht der Fall (Abb. 4). Hier bleibt der Schüler auf der Ebene der Mathematik.

Die Dokumentationen lassen erkennen, wann das CAS eingesetzt wurde. Die ersten beiden Lösungen tun dies, ohne explizit zu machen, auf welche Weise das CAS verwendet wurde. Um das zu verstehen, muss der Leser das nötige Wissen über das verwendete Werkzeug und seine Funktionalitäten bereits besitzen. Für die Kommunikation in einer Prüfung zwischen dem Prüfling und seinem Lehrer stellt dies im Allgemeinen kein Problem dar. In der dritten Bearbeitung werden explizit die Befehle angegeben, die verwendet werden (vgl. Abb. 4). In ihnen ist ebenfalls die mathematische Idee enthalten.

In der ersten Lösung tritt der traditionelle Aufbau (wie bei der Lösung per Hand) deutlich hervor. Schritt für Schritt werden die erste und zweite Ableitung bestimmt und die (Teil-) Ergebnisse dokumentiert. Dann wird eine Gleichung aufgestellt und diese mithilfe des CAS gelöst. In der dritten Lösung ist sehr deutlich ersichtlich, wie die CAS-Verweise überhand nehmen können und die mathematische Idee in den Hintergrund tritt.

Kategorien und was sie leisten können

Bei der Analyse von Schülertexten (Abiturlösungen) wurden über die oben genannten (kursive Begriffe) hinaus noch folgende Kategorien herausgearbeitet, die als Bestandteile der Texte auftreten:

Mathematische Idee
Rechnereinsatz
Erklärungen
Strukturierungselemente
Ergebnisse

Für die obige Aufgabe könnte eine Dokumentation z.B. so aussehen.

Diese Kategorien können einerseits dazu dienen, eine Schülerlösung zu beschreiben. Andererseits können sie Lehrerinnen und Lehrern dabei helfen, über Lösungsdokumentationen zu reflektieren und bewusster „mathematische Texte” zu verfassen. Dazu gehören auch Strukturierungselemente, also Bestandteile, die dabei helfen, die zu vermittelnde Information zu organisieren. Von Schülerinnen und Schülern werden am häufigsten Zeilenumbrüche und Pfeile verwendet, um zu verdeutlichen, was der nächste Schritt oder das Ergebnis der vorherigen Tätigkeit ist. Vor allem mathematisch-logische Folgepfeile werden dabei mit einer anderen Bedeutung gebraucht, als es in der Fachwissenschaft üblich ist. Außerdem lassen sich Beispiellösungen auf Grundlage der Kategorien systematisch erstellen.

Es kann wohl nicht erwartet werden, dass Schülerinnen und Schüler in dieser sprachlich sehr ausführlichen Form dokumentieren werden. Das Beispiel soll vielmehr Lehrerinnen und Lehrern helfen, den Blick zu schärfen und die eigene Einstellung gegenüber dem, was eine Lösungsdokumentation ausmacht, zu reflektieren. In diesem Sinne ist dieses Beispiel auch kein „Musterbeispiel“, sondern ein Anhaltspunkt, worauf zu achten sein könnte. Hier wurde bewusst auf die Notation von CAS-Befehlen verzichtet, aber je nach Zweck der Dokumentation oder Vertrautheit des Befehls könnte dies auch anders gehandhabt werden.

Ausblick

Der Kern einer Dokumentation umfasst die mathematischen Ideen, die zur Lösung einer Aufgabe beitragen. Auf diesen sollte in jedem Fall der Schwerpunkt liegen. Darüber hinaus sind außerdem verbalisierte Erklärungen hilfreich, um Zusammenhänge zu verstehen bzw. (aus Schülersicht) diese herzustellen. Ziel sollte es sein, den Anteil an mathematischer Fachsprache sukzessive zu erhöhen. Dies muss von Lehrerinnen und Lehrern gleichermaßen gefordert und gefördert werden.

Literatur

Barzel, B., Hußmann, S. & Leuders, T. (2005). Computer, Internet & Co. im Mathematikunterricht. Berlin: Cornelsen Scriptor.

Beck, C. & Maier, H. (1996). Zu Methoden der Textinterpretation in der empirischen mathematikdidaktischen Forschung. In Maier, H., Voigt, J. Arbeiten zur interpretativen Unterrichtsforschung. Köln: AulisVerlag Deubner. S. 43-76.

Beck, J. (2015). Schülererklärungen in Lösungsdokumentationen beim Einsatz von CAS in Prüfungen. In Caluori, F. Linneweber-Lammerskitten, H. Streit, C. Beiträge zum Mathematikunterricht 2015. Münster: WTM-Verlag. S. 120-124.

Pallack, A. (2007). „Die gute CAS-Aufgabe für die Prüfung”. In Beiträge zum Mathematikunterricht 2007. Hildesheim, Berlin: Franzbecker. S. 90-94.

Dieser Beitrag stammt ursprünglich aus dem Casio Forum 2017/1.