Mittels dynamischer Geometrie Software (DGS) können Zusammenhänge zwischen Größen von geometrischen Objekten untersucht werden. Darauf aufbauend lassen sich Überlegungen zu ganzen Klassen von Objekten anstellen. So können Schülerinnen und Schüler beispielsweise feststellen, dass in einem frei gewählten Dreieck \(ABC\) mit \(γ=90°\) die Beziehung \(a^2+b^2=c^2\) gilt.
Ein Beitrag von Manuel García Mateos, Gymnasium am Steinwald in Neunkirchen
– MaLeNe-Koordinator Saarland –

Während das auch ohne größeren Aufwand mit einer einzelnen Zeichnung möglich ist, bietet DGS die Möglichkeit bei konstantem Winkel \(γ=90°\) den anliegenden Punkt zu verschieben und die Flächen automatisiert neu zu bestimmen (vgl. Abb. 1). Auch die anderen Punkte des Dreiecks können verschoben und mit konstantem Winkel untersucht werden. Auf diese Weise lassen sich beliebig viele Dreiecke untersuchen, die die Hypothese nahelegen, dass die Summe der Quadrate über den Katheten stets dem Quadrat über der Hypotenuse (Satz des Pythagoras) gilt. Die Frage, ob das wirklich immer gilt, lässt sich in einem anschließenden Beweis sichern.
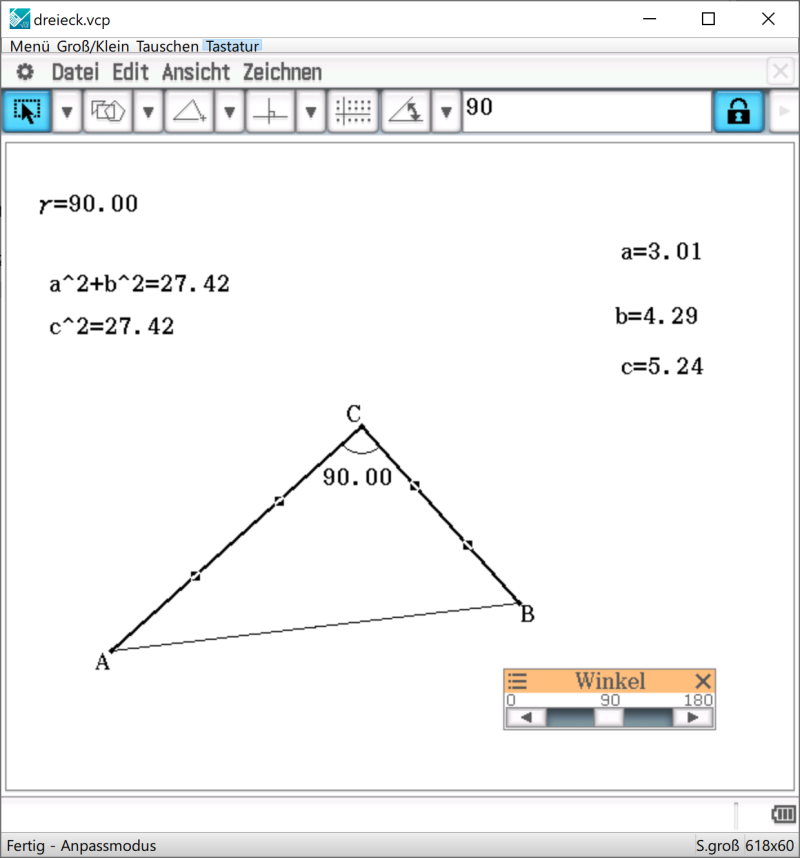
Auf ähnliche Weise lassen sich auch weitere Sätze der Satzgruppe, nämlich der Höhensatz von Euklid („Wenn das Dreieck ABC rechtwinklig ist mit \(γ=90°\) und den Hypotenusenabschnitten \(p\) und \(q\), dann gilt für die Höhe über der Hypotenuse die Beziehung \(h^2=p⋅ q\).“) und der Kathetensatz von Euklid („Das Quadrat über der Kathete ist flächengleich zum Rechteck aus der Hypotenuse und dem anliegenden Hypotenusenabschnitt.“) darstellen.
Eine weitere Entdeckung lässt sich aber auch mit dem ClassPad durch den Einsatz von Formeltermen und Schiebereglern machen.
Es gilt: „Wenn das Dreieck ABC rechtwinklig ist mit \(γ=90°\), dann gilt \((\frac{1}{a})^2+(\frac{1}{b})^2=(\frac{1}{h_c})^2\), wobei \(h_c\) die Höhe über der Hypotenuse darstellt.“
Auch hier ist übrigens der Kehrsatz „Wenn \((\frac{1}{a})^2+(\frac{1}{b})^2=(\frac{1}{h_c})^2\) gilt, dann ist das Dreieck rechtwinklig mit \(γ=90°\)“.
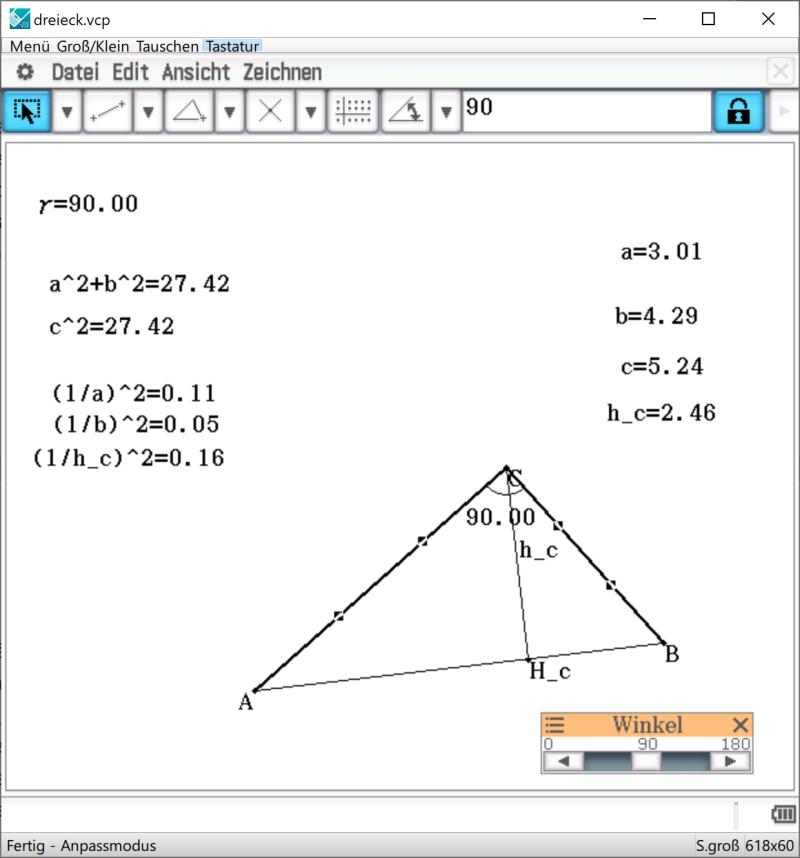
Diese Untersuchungen regen dazu an, weitere Fragen zu formulieren und zu formulieren. Die Sachverhalte können entsprechend dargestellt werden, es können Vermutungen geäußert und anschließend untersucht werden. Man könnte z. B. fragen, ob es Winkel oder Streckenlängen gibt, so dass \((\frac{1}{a})^2+(\frac{1}{b})^2=(\frac{1}{c})^2\) ist.









