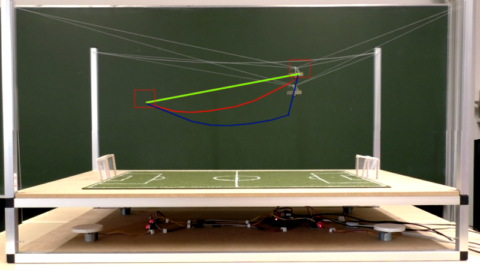
Camcarpets sind vor allem aus Fußballstadien bekannt. Meist hinter der Torauslinie liegen auf dem Rasen Werbefolien, die aus der Perspektive der Hauptkamera wie stehende, dreidimensionale Buchstaben wirken. Solche Folien können mit Schülerinnen und Schülern beim Einstieg in die dreidimensionale Geometrie selbst erstellt werden und bieten eine gute Gelegenheit für einen handlungsaktiven Unterricht.

Eine Unterrichtsidee von Henning Franzen, Fördegymnasium Flensburg
– MaLeNe-Koordinator Schleswig-Holstein –

Bei dem Projekt werden lediglich Methoden und Kenntnisse gefordert und gefördert, die im Zentrum des Lehrplans stehen, weshalb es sich gut in den Regelunterricht integrieren lässt, ohne zusätzliche zeitliche Ressourcen zu beanspruchen.

Um nachzuvollziehen, welche Chancen sich hier bieten, wird empfohlen, nach der folgenden Anleitung einen einfachen Camcarpet, zum Beispiel zur Darstellung eines Quaders, selbst herzustellen. Beim Basteln erfährt man, welches mathematische Handwerk, vor allem aber welches Orientierungsvermögen gefragt bzw. trainiert wird. Auch für uns Lehrkräfte ergeben sich dabei Momente, in denen wir etwas grübeln müssen.

Im Wesentlichen müssen folgende Schritte abgearbeitet werden:

1. Dreidimensionale Planung des ganzen Szenarios:

Lege ein Koordinatensystem für den Raum fest.
Lege die Position der Kamera (Blickpunkt) fest.
Wähle ein Objekt, dessen Eindruck erweckt werden soll (im obigen Bildbeispiel der Buchstabe W), und die Position, auf der er erscheinen soll. Wähle bzw. ermittle dazu die Koordinaten eines jeden Eckpunktes dieses Objekts.

2. Stelle für jeden dieser Eckpunkte die Verbindungsgerade mit der Kameraposition auf und berechne den Durchstoßpunkt mit der Fußbodenebene.

3. Zeichne die Durchstoßpunkte auf ein Blatt und verbinde sie entsprechend ihres Modells.

Camcarpets eignen sich als handlungsaktive Übung zum Ende der Unterrichtseinheit. Sie bieten sich aber – bei Ergänzung durch andere Basteleien mit Perspektiveffekten (s.u.) – sehr gut als Leitmotiv für die gesamte Einheit an, ohne dass die Lehrkraft ihr gewohntes Vorgehen wesentlich ändern muss: Steigt man mit einem Szenario wie dem obigen in das Thema ein, kommen die Lernenden fast von allein auf die Notwendigkeit eines dreidimensionalen Koordinatensystems und der Orientierung in diesem. Hier führt die Lehrkraft die Vektoren ein. Die Frage nach der Streckung des Verbindungsvektors von Kamerapunkt und Eckpunkt kann zur Idee der Geradengleichung führen.

Eine allmähliche Erhöhung des Schwierigkeitsgrads erreicht man durch Projekte wie das “H” und die “Flagge” (siehe Bilder). Die Grundidee und die Rechenwege sind dieselben, hier müssen aber mehr und (für Einsteiger) kompliziertere Ebenengleichungen aufgestellt werden. Zudem taucht hier bereits die klassische Abiturfrage auf, ob der Durchstoßpunkt von Gerade und Ebene auch im jeweils betrachteten Ausschnitt der Ebene liegt.

Es ist überraschend, auf wie viele Ideen für ähnliche Basteleien man kommen kann, wenn die ersten Schritte gemacht sind. Auch Aufgaben mit Abständen und Flächeninhalten lassen sich fast von selbst aus dem Setting ableiten.

Beim Erstellen solcher Objekte müssen viele Durchstoßpunkte berechnet werden. Die dabei entstehenden Punktkoordinaten sind praktisch immer Dezimalbrüche mit vielen Nachkommastellen. Ohne Rechnerunterstützung wird das also eine mühselige, zeitraubende und damit demotivierende Angelegenheit. Durch den Einsatz von CAS oder GTR spart man aber nicht nur Zeit und Mühen. Die Interpretation der Ergebnisse und deren “Umsetzung” in die Realität bekommen einen höheren Stellenwert. Und der reine Rechenweg, der per Hand natürlich beherrscht werden soll, wird als das erkannt, was er ist: ein Algorithmus.