In amerikanischen Schulbüchern zur elementaren Statistik ist folgende anwendungsorientierte und historisch belegte Aufgabenstellung zu finden: Das Dolbearsche Gesetz (Dolbear’s Law) beschreibt den Zusammenhang zwischen der Umgebungstemperatur und der Zirprate einer fast überall in den USA vorkommenden Grille, der zu den Blütengrillen gehörenden Oecanthus fultoni (Snowy Tree Cricket), die deshalb auch als Thermometergrille (Thermometer Cricket) bezeichnet wird.

Ein Artikel von Prof. Dr. Ludwig Paditz, HTW Dresden

Das „Gesetz“ wurde vom Physiker und Erfinder A.E. Dolbear (1837-1910) formuliert und 1897 in der Zeitschrift „American Naturalist“ unter dem Titel „The Cricket as a Thermometer“ publiziert.

In der heute verwendeten Form müssen die Zirprufe der Schneeweißen Blütengrille lediglich 15 Sekunden lang gezählt werden. Zu dieser Zahl wird 40 addiert, das ergibt die Temperatur am Standort der Grille – in Grad Fahrenheit.

Hörprobe (Video mit dem Gesang der Blütengrille)

Hörprobe (Video, Schallanalyse, Sonogramm)

Es sei N die Anzahl der Zirprufe pro Minute und T die Temperatur in °F. In der aktuellen heutigen Form des „Gesetzes“ T = 40 + N/4 steht der Term N/4 für die Anzahl der Zirprufe in 15 Sekunden.

Anhand von 15 Datenpaaren ( \(x_i\), \(y_i\) ) wird mithilfe der linearen Regression das Gesetz für eine andere Grillenart untersucht (\(x_i\) : Anzahl der gemessenen Zirprufe pro sec.; \(y_i\) : gemessene Temperatur in °F ).

Dolbear nutzte für seine Formel von 1897 den Datensatz listT:={50,60,70} und listN:={40,80,120}. Er berechnete mit dem „Gesetz“ die Temperatur für N=100 Zirprufe/min: T = 50 + (100 – 40) / 4 = 65 [°F].

Kontrolle mit dem ClassPad:

Dolbear erwähnte, dass sich bei Veränderung der Zirprufe um 4 pro min die Temperatur um 1°F geändert haben muss, er beobachtete damals die Schneeweiße Blütengrille.

G.W. Pierce im Labor mit dem von ihm entwickelten Schallmessgerät
(Havard University, Harvard University Archives W245865_1)

Der Datensatz von Pierce (1948)
Pierce geht in seinem Buch „The Songs of Insects“ darauf ein, dass unterschiedliche Arten von Grillen mit verschiedenen Frequenzen
zirpen, der lineare Zusammenhang – wie von Dolbear vermutet – aber erhalten bleibt.

Hörprobe (Bodengrille, Video, Schallanalyse, Sonogramm)

Die Daten wurden aus dem Schulbuch „Elementary Statistics“ von R. Johnson und P. Kuby (11. Auflage 2012, ISBN 978-0-8400-5389-3) entnommen, gemessen wurde die „Gestreifte Bodengrille“ Striped
Ground Cricket, Allonemobius fasciatus) :
listx:={20,16,19.8,18.4,17.1,15.5,14.7,17.1,15.4,16.2,15,17.2,16,17,14.4}
listy:={88.6,71.6,93.3,84.3,80.6,75.2,69.7,82,69.4,83.3,79.6,82.6,80.6,83.5,76.3}

Darstellung der Datenpunkte als Punkteplot in der x-y-Ebene:

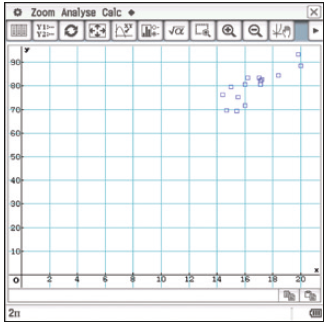
Lineare Regression: \(y(x) = 25.2 + 3.3x\)

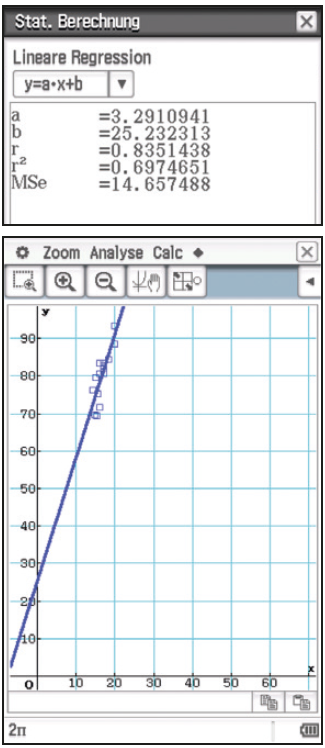
Auch für diese Grillenart ist ein linearer Zusammenhang gegeben, eine hohe Korrelation zwischen listx und listy besteht: r=0.8351. Das Bestimmtheitsmaß (r²=69,7%) sagt aus, dass ca. 70% des Zusammenhanges
von Zirprate und Temperatur durch das lineare Regressionsmodell erklärt werden. Die Streuung der Datenpunkte um die Regressionsgerade kann zufallsbedingt sein (z.B. Messfehler).

Für das gegebene Datenmaterial bieten sich weitere Aufgaben aus dem oben zitierten Schulbuch an:

Describe the pattern displayed. (strongly linearly increasing)
Using the linear equation, find the temperatures that correspond to 14 and 20 chirps, the approximate bounds for the domain of the study. (71°F and 91°F)
Does the range of temperature values bounded by the temperature values found in part 2 seem reasonable for this study? Explain. (Temperature range from 70°F to 90°F on summer nights.)
The next time you are out where crickets chirp on a summer night and you find yourself without a thermometer, just count the chirps and you will be able to tell the temperature. If the count is 16, what temperature would you suspect it is? (78°F)