In diesem Beitrag geht es darum, eine Funktion mit elementaren Methoden der Sekundarstufe I an Messwerte anzupassen.
Ein Artikel von Michael Bostelmann, Mons-Tabor-Gymnasium Montabaur

1. Messung
Um den Zusammenhang zwischen Durchmesser d und Umfang U eines Kreises zu untersuchen, werden Euro-Münzen vermessen. Die Messung des Umfangs ist gar nicht so einfach, sodass hier ein relativ großer Messfehler entsteht. Dies ist durchaus beabsichtigt, da es um die Auswertung von
fehlerbehafteten Daten geht.
Das Ergebnis könnte so aussehen:
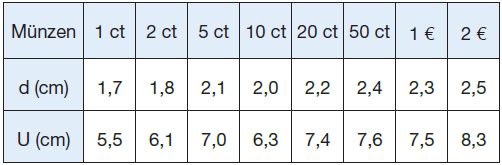
2. Auswertung
Gesucht ist eine Funktion U, die den Zusammenhang zwischen Durchmesser d und Umfang U möglichst gut beschreibt. Was genau „möglichst gut“ bedeutet, wird erst im weiteren Verlauf der Reihe quantitativ betrachtet. Vorerst vertrauen wir auf ein qualitatives „Bauchgefühl“. Eine erste Modell-Vermutung legt die grafische Darstellung nahe.
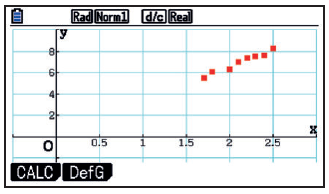
Da es um „möglichst gut“ und nicht um „exakt“ geht, darf die erste Frage nicht lauten: „Liegen die Punkte auf einer Geraden?“, sondern eher: „Liegen die Punkte auf einer geraden Straße, oder macht diese eher eine Links- bzw. Rechtskurve?“. Bei der Beantwortung dieser Frage hilft der „schräge Blick“. Dabei wird etwa vom Koordinatenursprung aus flach über den Plot geblickt.
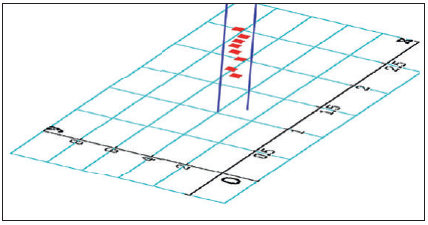
Ein lineares Modell erscheint passend. Die zweite Frage könnte dann lauten “Ist ein proportionales Modell sinnvoll?”. In diesem Fall haben die Schülerinnen und Schüler die Frage mit „Ja“ beantwortet, da eine Münze mit Durchmesser null auch den Umfang null haben sollte. Dies führt zu einem proportionalen Modell:
$$U(d) = k \cdot d$$
Damit ergibt sich als erstes Ergebnis:
Bei einem Kreis sind Umfang und Durchmesser proportional.
2.1. Regression durch Mittelwertbildung
Um den Proportionalitätsfaktor \(k\) zu bestimmen, kann die Quotientengleichheit bei der proportionalen Zuordnung genutzt werden. Da da Experiment im Unterricht nach der Behandlung der proportionalen Zuordnungen durchgeführt wurde, bildeten die Schülerinnen und Schüler in den meisten Fällen für jedes Messwertpaar den Quotienten \(k\) und berechneten daraus den Mittelwert \(\overline{k}\). Nur einmal wurde dabei eine zweite Variante gewählt. Dabei wurden zuerst die Mittelwerte \(\overline{d}\) der Durchmesser und \(\overline{U}\) der Umfänge gebildet und daraus der Quotient berechnet.
So ergab sich dann:
$$U_{1}(d) = \overline{k}\cdot d \approx 3,28\cdot d$$
bzw.
$$U_{2}(d) = \frac{6,96cm}{2,13cm}\cdot d \approx 3,27\cdot d$$
Ein Regressionsmodul liefert ebenfalls den Wert \(k \approx 3,28\).
Der grafische Vergleich zeigt, dass sich die beiden Modelle nur unwesentlich unterscheiden.
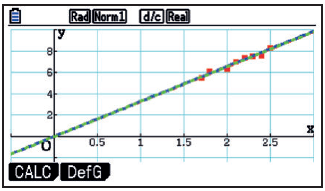
Ergebnisse grün: U(d)=3,27x
Als Proportionalitätsfaktor erhielten wir \(k\approx 3,28\) bzw. \(k\approx 3,27\). Abb. 3 zeigt eine optisch gute Anpassung des Modells an die Messwerte. So ergab sich im Unterricht auch keine Notwendigkeit, ein quantitatives Gütekriterium einzuführen.
Entscheidend bei diesem Experiment ist die Modellstruktur, also die Proportionalität zwischen Durchmesser und Umfang beim Kreis. Der Proportionalitätsfaktor \(k=3,28\) fällt quasi als „Beifang“ mit ab und wäre für die Schulpraxis durchaus brauchbar. Hier lohnt sich ein kleiner historischer Exkurs über die Geschichte der Kreiszahl \(\pi\). Natürlich kann später der im Taschenrechner gespeicherte Wert für \(\pi\) verwendet werden.
Damit haben wir eine einfache Methode gefunden, wie rechnerisch eine proportionale Regression durchzuführen ist, die alle Messwerte mit einbezieht. Nicht berücksichtigt wurden dabei die Messfehler bei Umfang und Durchmesser sowie der Fehler des Proportionalitätsfaktors. Regressionsmodule berücksichtigen diese Fehler in der Regel nicht, eine Berechnung ist mit den Mitteln der Sekundarstufe I auch nicht möglich. Es gibt aber eine einfache geometrische Methode, mit der sich solche Fehler abschätzen lassen.
2.2 Regression mithilfe von Fehlerbalken bzw. -rechtecken
Zunächst wird der Messfehler für die beiden Größen Umfang U und Durchmesser d geschätzt. Die von den Schülerinnen und Schülern angenommenen Fehler betrugen 1mm bei d und 3 mm bei U. Im Koordinatensystem werden an den Messwertpunkten Fehlerbalken eingezeichnet, die die Schwankungen darstellen. Dadurch entstehen Fehlerkreuze, die jeweils ein Fehlerrechteck aufspannen. Bei einer proportionalen Regression werden nun zwei Ursprungsgeraden \(s_{min}\) bzw. \(s_{max}\) so gezeichnet, dass sie durch alle Fehlerrechtecke gehen und minimale bzw. maximale Steigung haben.
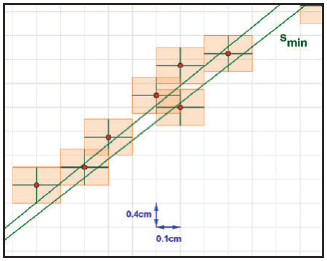
Mithilfe geeigneter Steigungsdreiecke lassen sich die Steigungen von \(s_{min}\) und \(s_{max}\) ermitteln. Als Schätzwert für den Proportionalitätsfaktor kann der Mittelwert daraus verwendet werden. Die Steigungen von \(s_{min}\) bzw. \(s_{max}\) bilden dann den unteren bzw. oberen Rand des Fehlerintervalls.
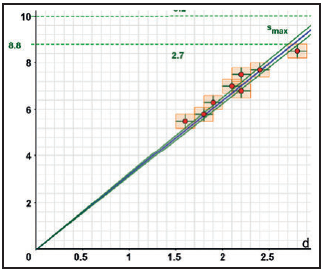
\(s_{min}:U(d)=\frac{10}{3,2}d=3,125d\)
\(s_{max}:U(d)=\frac{8,8}{2,7}d\approx3,259d\)
Mittelwert: \(\frac{3,125+3,259}{2}\approx3,19\)
Intervallradius: \(\frac{3,259-3,125}{2}\approx0,07\)
Also wäre das Ergebnis: \(U(d)=k \cdot d\) mit \(k=3,19 \pm 0,07\)
Dieses Verfahren lässt sich auch auf eine lineare Regression erweitern, worauf allerdings hier nicht weiter eingegangen wird.
3. Fazit
Es wurden zwei Verfahren vorgestellt, mit denen bereits in der Sekundarstufe I eine proportionale Regression durchgeführt werden kann. Damit lässt sich bereits ein großer Teil der in den Naturwissenschaften vorkommenden Experimente auswerten, da hier häufig proportionale Beziehungen auftreten (Ohmsches Gesetz: \(U \sim I\), Hooksches Gesetz: \(F \sim s\), thermische Längenausdehnung: \(\Delta l \sim \Delta \vartheta\), …). In manchen Fällen tritt die Proportionalität nicht direkt zwischen zwei Größen auf, lässt sich aber entsprechend modifizieren (Freier Fall: \(h \sim t^2\), Pendelschwingung: \(T \sim \sqrt{l}\). Somit haben proportionale Modelle und die damit verbundene proportionale Regression eine große Reichweite.
Dieser Beitrag stammt ursprünglich aus dem Casio Forum 2020/2.
Forum
Dieser Beitrag kann hier diskutiert werden:
https://mathematik-lehr-netzwerk.de/community/blogb/regression-mit-elementaren-methoden-in-der-sekundarstufe-i/