Ortungsdienste im Handy, Routenplanung oder Navigationssysteme, all diese Applikationen verwenden das GPS-Satellitensystem für die Bestimmung der eigenen Position. Wie dies passiert, kann mathematisch in der Sekundarstufe II thematisiert werden, auch wenn die dahinterstehenden Berechnungen aufwendig sind. Dieses Thema ist geeignet, den Schülern eine echte mathematische Modellierung zu bieten und um CAS sinnvoll im Mathematikunterricht einzusetzen.
Ein Beitrag von Dr. Kinga Szücs, Universität Erfurt

Das Global Positioning System (GPS)
Das für militärische Zwecke entwickelte System besteht aus 24 Satelliten, die auf sechs Kreisbahnen in einer Höhe von ca. 20.000 km mit gleicher Geschwindigkeit die Erde umkreisen. Die Anordnung der Satelliten gewährleistet, dass jeder Punkt auf der Erde immer durch mindestens vier Satelliten angepeilt werden kann. Sie sind mit Atomuhren ausgestattet, so können sie ihre eigene Uhrzeit sehr genau senden. Stationen auf der Erde überwachen die Satelliten und die von ihnen gefunkten Daten. Jeder sendet ständig drei aktuelle Informationen: Name, Position und Uhrzeit. Aus diesen Daten ermitteln dann die Endgeräte die Position des Empfängers.
Was machen die Endgeräte?
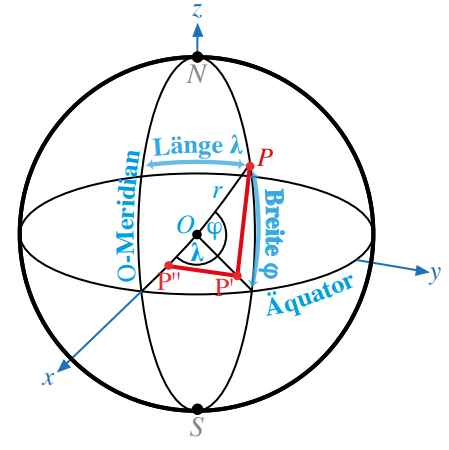
Die Satelliten senden ihre eigene Position nicht in geografischen Koordinaten, sondern in einem kartesischen Koordinatensystem, dem World Geodetic System (WGS). Der Ursprung des WGS liegt im Massenschwerpunkt der Erde, ihre Rotationsachse ist die z-Achse des WGS. Die x-Achse geht durch den Schnittpunkt des Nullmeridians mit dem Äquator und die y-Achse ergänzt diese Achsen zu einem orthogonalen Rechtssystem (Abb. 1). Die Endgeräte berechnen aus der Differenz der eigenen und der empfangenen Uhrzeit, wie lange das Signal mit Lichtgeschwindigkeit unterwegs war und daraus die Entfernung zum Satelliten. Alle Punkte im Raum, die von einem festen Punkt (=Satellit) einen festen Abstand haben, liegen auf einer Kugeloberfläche; Mittelpunkt ist der Satellit, der berechnete Abstand der Radius: eine erste Kugelgleichung für die eigene Position. Da nicht nur ein Signal, sondern mindestens vier gleichzeitig empfangen werden, gibt es ein Gleichungssystem mit drei Unbekannten und mindestens vier Quadratischen Gleichungen, die Lösung ist die Position des Empfängers – geometrisch gesehen der Schnittpunkt der Kugeloberflächen. Diese Lösung wird in geografische Koordinaten umgerechnet (Abb. 1).
Da die Position des Empfängers auf der Erdoberfläche liegt, kann noch eine Gleichung dem System hinzugefügt werden. Deswegen könnten die Signale dreier Satelliten für die Positionsbestimmung ausreichen. Wegen des sogenannten Uhrenfehlers sind aber die Daten von vier Satelliten nötig.
Bestimmung der eigenen Position aus empfangenen GPS-Daten
Die folgende Aufgabe wurde in Anlehnung an Rascher-Friesenhausen, 2004, formuliert, auch die verwendeten Daten entstammen dieser Quelle.
Ein GPS-Gerät empfängt die Signale der vier Satelliten: F3(II 06), C4(II A20), A4(II 04), D1(II A11). Bestimmen Sie die Position des Empfängers. (Die Lichtgeschwindigkeit beträgt 299.792,458 km/s).
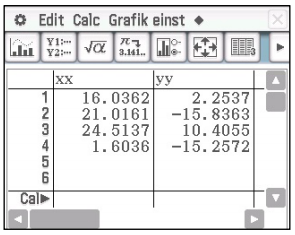

Abb. 2: Empfangene GPS-Daten: xx, yy, und zz in 1000 km, Laufzeit dt in msec
Es wird ein Gleichungssystem in dieser Notation benötigt (vgl. Gleichung der Kugelfläche):
\((x-xx[n])^2+(y-yy[n])^2+(z-zz[n])^2=r[n]^2\) mit \(r[n]=\frac{d[n]}{1000}\cdot 299.792,458\)

In einem ersten Schritt werden die Quadrate der Entfernungen der Satelliten zum Empfänger aus der Zeit bestimmt und die Position der Satelliten quadratisch auf die Empfängerposition bezogen (Abb. 3). Dann wird damit das Gleichungssystem aufgestellt:

Da ein System von vier quadratischen Gleichungen vorliegt, wird das CAS entweder „No solution“ ausgeben oder „ewig“ an einer Lösung arbeiten. Das System muss auf jeden Fall eine Lösung haben! Ein möglicher Trick ist die Linearisierung des Systems: Wird die Differenz von je zwei verschiedenen Gleichungen gebildet, so entfallen die quadratischen Terme und die Anzahl der Gleichungen reduziert sich auf drei! Dieses Gleichungssystem wird wie gewohnt rasch gelöst (Abb. 5).

Nun ist die Position des Empfängers im kartesischen WGS-System bestimmt, sie wird noch in geografische Koordinaten umgerechnet.
Umrechnung von WGS-Koordinaten in geografische Koordinaten
Jeder Punkt \(P\) auf der Erde kann durch die Daten \(\varphi\), \(\lambda\) und \(r\) eindeutig angegeben werden, wobei \(\varphi\) die geographische Breite, \(\lambda\) die geographische Länge und \(r\) die Entfernung des Punktes vom Erdmassenschwerpunkt \(O\) angibt (Abb. 1). Letztere entspricht meistens dem Erdradius, in einem Flugzeug können sich messbare Abweichungen ergeben.
Sei \(P’\) die orthogonale Projektion des Punktes \(P’\) auf die \(x\)-\(y\)-Ebende und \(r=OP’\) sowie \(P^{\prime\prime}\) die orthogonale Projektion des Punktes \(P’\) auf die \(x\)-Achse. Dann gilt für den Punkt \(P\), dass seine \(x\)-Koordinate der Strecke \(OP^{\prime\prime}\), die y-Koordinate der Strecke \(P’P^{\prime\prime}\) und die \(z\)-Koordinate der Strecke \(PP’\) entspricht.
Es gilt im rechtwinkligen Dreieck \(OP^{\prime\prime}P’\):
\(x=r’\cdot cos(\lambda)\) und \(y=r’\cdot sin(\lambda)\)
Im ebenfalls rechtwinkligen Dreieck \(OP’P\) gilt:
\(z=r\cdot sin(\varphi)\) und \(r’=r\cdot cos(\varphi)\)
Zusammengefasst:
$$\left(
\begin{array}{c}
x \\ y \\ z
\end{array} \right)
=r
\left(
\begin{array}{c}
cos(\varphi)\cdot cos(\lambda) \\ cos(\varphi)\cdot sin(\lambda) \\
sin(\varphi)
\end{array} \right)$$
Diese Gleichungen sind hilfreich, wenn die geographischen Koordinaten bekannt sind und daraus die WGS-Koordinaten ermittelt werden sollen. Für die Umkehrung ist wichtig, dass
\(r= \sqrt{x^2+y^2+z^2}\), \(sin(\varphi)= \frac{z}{r}\) und \(\frac{y}{x}=tan(\lambda)\).
Damit können die geographischen Koordinaten des Empfängers ermittelt werden. Zuerst wird die Entfernung vom Erdmassenmittelpunkt \(O\) mithilfe der zuvor ermittelten Lösung [ans] bestimmt (Abb. 6). Das Ergebnis entspricht ungefähr dem Erdradius.
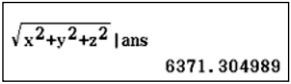
Nun werden die geographische Breite \(\varphi\) und die geographische Länge \(\lambda\) bestimmt (Abb. 7) [Rechner auf das Gradmaß umstellen].

Der Ort mit der nördlichen Breite 48,74° und der östlichen Länge 9,32° ist Esslingen.
Literatur
Rascher-Friesenhausen, R. (2004): Orientieren mit Mathematik. In: Mathematik lehren 124, S. 58-62.
Dieser Beitrag stammt ursprünglich aus dem Casio Forum 2018/2.
Forum
Dieser Beitrag kann hier diskutiert werden:
https://mathematik-lehr-netzwerk.de/community/blogb/gps-positionsbestimmung-mit-einem-cas/